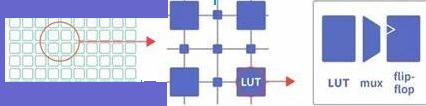
FPGA based Digital World

Welcome to FPGA based Digital World.
Signal processing is much important. |
Fourier Transform(FT)
An aperiodic signal can be thought of as periodic with infinite period, and could be expressed by integral of sinusoidals.
The Fourier transform is an integral tranform of aperiodic signal from time domain to frequency domain, as follows.
And the inverse Fourier transform is
The Fourier transform maps a function of time t to a complex-valued function of real-valued domain ¦Ø.
From Fourier Series to Fourier Transform
Take below aperiodic signal s(t) as example.
It could be supposed to be the extension of below rectangular wave with period T-->¡Þ.
The Fourier series is
and it could evolve to Fourier transform as below.
Properites of Fourier Transform
1 Linearity
2 Time Scaling
3 Time shifting
4 Frequency shifting(Amplitude Modulation)
5 Time Differentiation
6 Time Integration
7 Reversal
8 Duality
10 Convolution
where, * is convolution.
Fourier Transform Paris
The function f(t) and its transform F(¦Ø) form the Fourier transform Pairs.
¦Äfunction
Rectangular Function
Sampling Signal
Parseval's Theroem
Parseval's Theroem relates the energy carried by a signal to thr Fourier transform of the signal, as below.
It applies to both periodic and aperiodic signals.
| Altera/Intel | Xilinx | Lattice | Learn About Electronics |
| MircoSemi | Terasic | Electric Fans |
| All rights reserved by fpgadig.org |