FPGA Based Digital World - Frequency Response of a Sinusoidal Circuit

Frequency Response of a Sinusoidal Circuit

A sinusoidal signal has three parameters: 1) amplitude 2)phase 3)frequency.

In sinusodial circuit analysis,

- If source frequency remains constant, phasor method is employed to find the ciruit's gain and phase behavior;

- If source amplitude remains constant, frequency response is employed to find the circuit's dynamic behavior as a function of frequency.

The frequency response of a circuit is the variation in its behavior wiht change in signal frequency.

Two methods are employed to describe the circuit's frequency response.

1) Transfer function

2) Bode plot

Transfer Function

The transfer function H(ω) of a circuit is the freqeuency dependent ratio of a phasor output Y(ω) to a phasor input X(ω) of the circuit.

Transfer Function

Note:

1) H(ω) is a complex number with magnitude H(ω) and phase Ф. -->Both the repsonse's magnitude and phase could be different from the input signals';

2) The input and output can be either voltage or current, but not power.

3) The frequency response of a circuit is the plot of the transfer function H(ω) versus ω, with ω varifying from 0 to ∞.

The transfer function can be simplified as

simplified transfer function

where, N(ω) is the numerator polynomial part of H(ω),

D(ω) is the denominator polynomial part of H(ω).

The roots of N(ω)=0 are called zeros of H(ω), expressed as z1, z2, ...;

The roots of D(ω)=0 are called poles of H(ω), expressed as p1, p2,...

Below seven types of different factors can appear in various combinations in a transfer function:

1 Gain K

Zeros

2 zero (jω) at the origin

3 Simple zero (1+jω/z1)

4 Quadratic zero

Poles

5 Pole 1/(jω)at the origin

6 Simple pole 1/(1+jω/p1)

7 Quadratic pole

They have different inflence to the frequency response and will be discussed in Bode plot.

Decibel Scale and Bode Plot

Bel is the ratio of two levels of power

Ratio in bel = lg(P2/P1)

and decibel(dB) is 1/10th of a bel

Ratio in dB = 10lg(P2/P1)

For a four-terminal network with input and output resistance to be the same, or for the same resistor, the ratio is

Ratio in dB = 20lg(V2/V1) = 20lg(I2/I1)

Bode plot is a semilogarithm plot, where

- X axis; lg(ω)

- Y axis:

for magnitude: H(ω) in dB = 20lg( H(ω)), where H(ω) = mag( H(ω) )

for phase: in degree

as shown in below diagram.

bode plot

Simetrix is a powerful tool to find the bode plot of a circuit.

Bode Plot of Transfer Function

As mentioned in above, there're seven types of different factors in a transfer function.

Each factor can be ploted separately and then added graphically, because of logarithms involved.

The influence to the transfer function of each factor is to be discussed below, to help understand the theoretical analysis afterwards.

1 Constant gain K

Magnitude; 20lgK , Phase :0 degree

constant K

2 Zero at Origin(jω)

Magnitude: 20lg(ω) , Phase :90 degree

zero at origin

A sample circuit is shown below.

sample

Its transfer function is calculated as

H(ω)= Vo/Vi = -jωRC=-jω

3 Simple zero(1+jω/Z1)

Magnitude:

magnitude

Phase:

phase

simple zero

A sample circuit is shown below.

sample

The transfer fuction is

H(ω)= Vo/Vi = -(1+jω)

4 Quadratic zero ( quaratic zero )

Magtitude

magnitude

Phase

phase

It has a similar curve as the simple pole, but with a magnitude slope of 40dB/dec, and a phase slope of 90°/dec.

quadratic zero

5 Pole at Origin(1/jω)

It has a similar property as in type 2,but with diffent polarity in Y axis.

Magnitude: -20lg(ω) , Phase :-90 degree

pole at origin

A sample circuit is shown below.

sample

Its transfer function is calculated as

H(ω)= Vo/Vi = -1/(jωRC)=-1/(jω)

6 Simple pole(1/(1+jω/p1))

It has a similar property as in type 3,but with diffent polarity in Y axis.

Magnitude:

magnitude

Phase:

phase

A sample circuit is shown below.

sample

The transfer fuction is

H(ω)= Vo/Vi = -1/(1+jω)

7 Quadratic pole ()

Magnitude

magnitude

Phase

phase

Below is a summary of the transfer function curves.

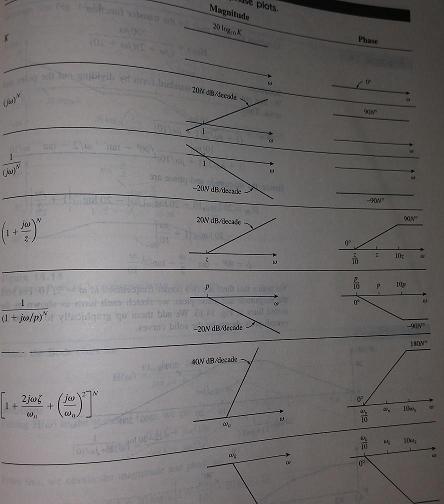
bode plot summary

[Summary]

1 Zero acts as a feedforward path to the circuit;

2 At zero, the magnitude is increased(+3dB) , and increases at the slope of N* 20dB/dec;And the phase is increased ( N*45°);

3 At pole, the magnitude is dereased(-3dB) ,and decreases at the slope of N* 20dB/dec.And the phase is decreased( - N*45°).


Altera/Intel	Xilinx	Lattice	Learn About Electronics
MircoSemi	Terasic	Electric Fans